7444. Graph game

Given graph, with 2n vertices and m edges. On every vertex and edge written an integer number. Serik and Zhomart were bored and invented the game on graph. The rules of this game are the following:

· Serik starts the game and they alternate turns.

· There are exactly n turns for each player.

· In every turn Player must choose a non-chosen vertex.

· The score of the player is the sum of numbers written in his chosen vertices, plus the sum of numbers written in edge, where both vertices of the edge are chosen by him.

· Every player tries to maximize the difference between his and opponent's score.

· Of course, Serik and Zhomart are very smart.

Input. The first line contains integers n, m (1 ≤ n, m ≤ 10⁵).

The second line contains integers a₁, a₂, . . . , a_2n (1 ≤ a_i ≤ 1000) – numbers on vertices.

Next m lines contain three integer numbers u, v, w (1 ≤ u, v ≤ n, 1 ≤ w ≤ 1000) – vertices u and v are connected, w is number on this edge. Only restriction for graph is: no loop edge.

Output. Print the difference between Serik’s score and Zhomart’s score.

Sample input	Sample output
3 3 2 3 2 2 3 1 6 1 3 4 3 2 1 2 1	1

SOLUTION

greedy

Algorithm analysis

Let the original graph contains an edge (u, v) of weight w, and the numbers a_u and a_v are written on the vertices:

Construct a new graph in which each such edge will be replaced by

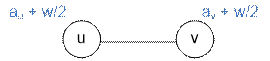
We transferred the edge weight to the vertex weights. If Serik and Zhomart start to play on the new graph, then the difference between the scores for the optimal game will be the same as on the original graph. Indeed, if vertex u is chosen by one of the guys, and vertex v by the other, then the difference between the number of received points will remain the same:

(a_v + w / 2) – (a_u + w / 2) = a_v – a_u

If both vertices are chosen by one of the game participants, then he will receive

(a_v + w / 2) + (a_u + w / 2) = a_v + a_u + w

points. That is, he will receive the numbers assigned to the vertices on the original graph plus the weight of the edge.

The optimal play on the new graph is greedy. Each of the participants on his turn must choose a vertex with the maximum value assigned to it.

Example

Consider the graph shown in the example. Let’s construct a new graph for it.

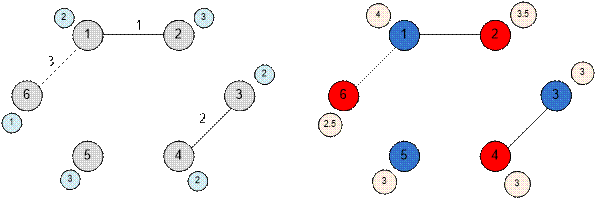
The first player will choose the vertices: 1, 3, 5 with weight 4 + 3 + 3 = 10.

The second player will choose the vertices: 2, 4, 6 with weight 3.5 + 3 + 2.5 = 9.

The difference between Serik’s score and Zhomart’s score is 10 – 9 = 1.

Algorithm realization

Store the numbers at the vertices of the graph in the array a.

#define MAX 200001

double a[MAX];

Read the input data.

scanf("%d %d", &n, &m);

n += n;

for (i = 1; i <= n; i++)

scanf("%lf", &a[i]);

Construct a new graph.

for (i = 1; i <= m; i++)

{

scanf("%d %d %d", &u, &v, &w);

a[u] += w / 2.0;

a[v] += w / 2.0;

}

Sort the array a in descending order.

sort(a + 1, a + n + 1, greater<double>());

Simulate the game – at each move the participant chooses the vertex with the maximum value.

double res = 0;

for (i = 1; i <= n; i++)

if (i & 1) res += a[i];

else res -= a[i];

Print the answer.

printf("%lld\n", (long long)res);